What is Pauli Exclusion Principle

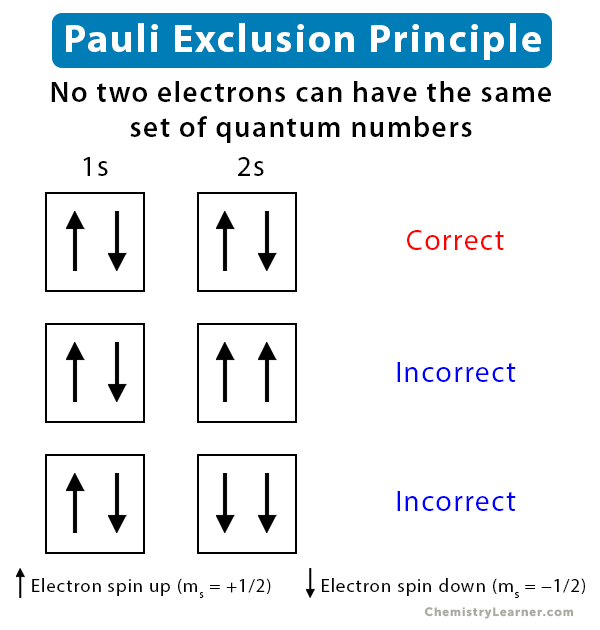
The state in which an electron resides in an atomic orbital is designated by a set of four quantum numbers – principal quantum number (n), azimuthal quantum number (l), magnetic quantum number (m_l), and spin quantum number (m_s). Pauli exclusion principle states that no two electrons can have the same set of quantum numbers.

According to Hund’s rule, each orbital of an atom’s subshell can have a maximum of two electrons. The two electrons have the same n, l, and m_l quantum numbers. However, they differ in the values of m_s. One electron has m_s = +1/2 and is in a “spin up” state. Another electron has m_s = -1/2 and is in a “spin down” state. These two electrons with opposite spins are said to be paired ^[1-5].

The discovery of the Pauli exclusion principle is credited to Austrian physicist and Noble laureate Wolfgang Pauli. He formulated this principle in 1925 for electrons and extended it to other fundamental particles in 1940.

Examples

The simplest example of Pauli exclusion principle is the helium atom, with two electrons in its 1s orbital. The first three quantum numbers are: n = 1, l = 0, and m_l = 0. Therefore, the two electrons have spin quantum numbers: m_s = +1/2 and m_s = -1/2 ^[1-4].

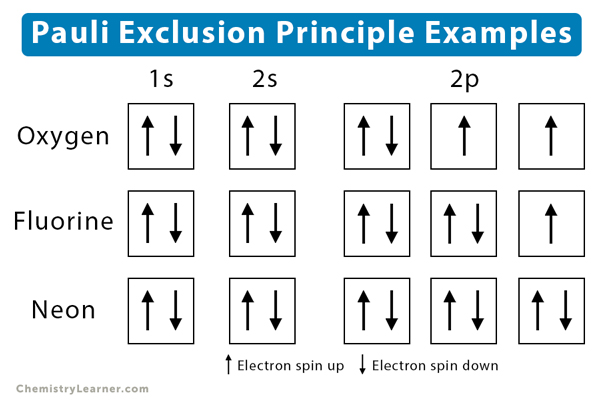
Similarly, the electron spins of oxygen, fluorine, and neon are illustrated below.

Applications

Pauli exclusion principle applies to a set of fundamental particles called Fermions that have half-integer spin (S = 1/2, 3/2, 5/2 …). These particles do not violate the principle. On the other hand, it does not apply to Bosons that have integer-spin (S = 1,2,3…). Pauli principle also applies to atoms with half-integer spin. For example, helium-3 has spin of +1/2.

Pauli exclusion principle can explain the electron-shell structure of atoms and the electron configuration of elements. It can explain how atoms form chemical bonds and how chemical properties vary among the elements. Hund’s rule uses the Pauli principle to fill up electrons in the various energy sublevels, thereby building up the periodic table elements.

Besides, this principle applies to quantum mechanics and astrophysics. In quantum mechanics, the Pauli exclusion principle states that Fermions must have an antisymmetric wave function, unlike Bosons, which have symmetric wavefunctions ^[1-3].