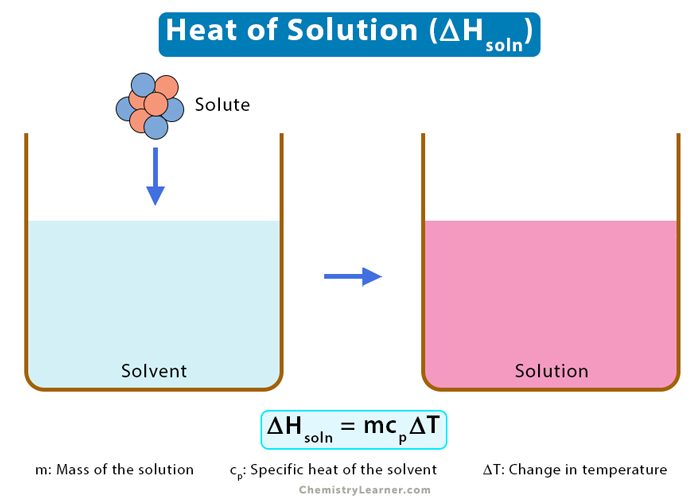
Heat of Solution
When a solute dissolves in a solvent, an enthalpy change occurs. The heat of solution is the difference in enthalpy between the dissolving solute and a solvent under constant pressure, resulting in infinite dilution. It is also known as the enthalpy of solution and is measured using a calorimeter. It can either be positive (endothermic) or negative (exothermic).
Hot and cold packs work due to the heat of solution of the chemicals inside these packs. These packs have an inner pouch that bursts when squeezed, allowing the chemical to dissolve in water. Heat is then released in the hot pack and absorbed in the cold pack.
The molar heat (enthalpy) of solution is the energy released or absorbed per mole of solute dissolved in a solvent.
Formula
The equation for the heat of solution is:
ΔHsoln = m x cp x ΔT
ΔHsoln: Heat of solution
m: Mass of the solution
cp: Specific heat of the solvent
ΔT: Temperature difference before and after the dissolution
How to Calculate Heat of Solution
To calculate the heat of solution, let us understand the steps involved in the dissolution process.
Step 1: Breaking of Solute
The intermolecular forces holding the solute molecules disappear, separating the molecules. As a result, the solute breaks up. It is an endothermic process since heat is supplied to break the bonds. Let ΔH1 be the enthalpy change and ΔH1 > 0.
Step 2: Breaking of Solvent
This process is similar to the breaking of solute. Heat must be supplied to break apart the solvent molecules. Let ΔH2 be the enthalpy change in this process and, just like before, ΔH2 > 0.
Step 3: Combination of Solute and Solvent Molecules
The third and final step is for the two types of molecules to combine and form a solution. Let ΔH3 be the enthalpy of combination and, since heat is released when two molecules combine to form a chemical bond, ΔH3 < 0. Therefore, the process is exothermic.
The sum of the enthalpies in each step gives the heat of solution.
ΔHsoln = ΔH1 + ΔH2 + ΔH3
The heat of solution can be greater than zero (ΔHsoln > 0) or less than zero (ΔHsoln < 0) depending upon the difference between ΔH1 + ΔH2 and ΔH3. If the heat of solution is equal to zero (ΔHsoln = 0), the solution is called an ideal solution. Otherwise, the solution is called a non-ideal solution.
For an ideal solution
ΔHsoln = ΔH1 + ΔH2 + ΔH3 = 0
=> ΔH1 + ΔH2 = – ΔH3
Example Problems
Problem 1. Calculate the heat of solution when 50 g of hydrated salt is dissolved in 100 g of water, resulting in a temperature increase of 20 °C. The specific heat of water is 4.184 J/g-°C.
Solution.
Given m = 50 g + 100 g = 150 g cp = 4.184 J/g-°C ΔT = 20 °C
The heat of solution is
ΔHsoln = m x cp x ΔT
=> ΔHsoln = 150 g x 4.184 J/g-°C x 20 °C
=> ΔHsoln = 12552 J or 12.6 kJ
Problem 2. 120 g of water experienced an increased temperature of 2 °C when 0.24 g of NaOH was dissolved. Calculate the enthalpy of solution in kJ/mol of NaOH. (Molar mass of NaOH is 40 g/mol, and the specific heat of water is 4.18 J/g-°C)
Solution
Given mNaoH = 0.24 g mwater = 120 g cp = 4.184 J/g-°C ΔT = 2 °C
The heat absorbed by the solution is
q = mwater x cp x ΔT
=> q = 120 g x 4.184 J/g-°C x 2 °C
=> q = 1004 J
The dissolution of NaOH gave 1004 J of energy. Therefore, ΔHsoln = -1004 J
Number of moles of NaOH: n = mNaOH /MNaOH = 0.24 g /40 g-mol-1 = 0.006 mol
The enthalpy of solution of 0.006 mol of NaOH is 1004 J
Therefore, the enthalpy of solution of 1 mol of NaOH is = 1004 J/0.006 mol = 167333 J/mol or 167.3 kJ/mol.