The heat of combustion is the heat released by a substance when it undergoes complete combustion in the presence of oxygen at standard temperature and pressure conditions. When the amount is quantified for one mole of the substance, we call it molar heat of combustion ^[1-4].

How to Calculate Heat of Combustion

The heat of combustion is calculated by using a bomb calorimeter. A stoichiometric mixture of fuel and oxidizer is kept in a steel container at 25 °C and initiated by an ignition device. The reaction is then allowed to complete. Hydrogen and oxygen react during combustion, producing water vapor. The vessel and its contents are then cooled to the original 25 °C. The heat of combustion is determined as the heat is released ^[1-3].

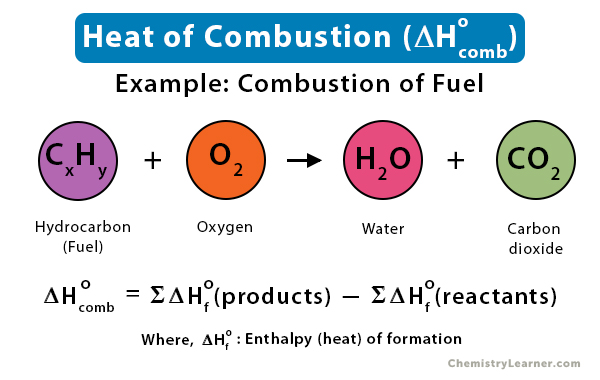
Formula

Theoretically, the heat of combustion is calculated from the difference between the heats of formation (ΔH_f^o) of the products and the reactants under standard conditions ^[1-3].

ΔH_comb^o = ΔH_f^o (products) – ΔH_f^o (reactants)

Symbol: ΔH_comb^o

Unit: Joules/mole (J/mol), Joules/gram (J/g), or J/m³

Standard conditions refer to a temperature of 25 ˚C and pressure of 10⁵ Pa.

Example

When fuels containing hydrocarbons are combusted in oxygen, the resulting products are carbon dioxide and water. A large amount of energy is released in the process. Let us look at a few examples ^[1-3].

1. Methanol (CH₃OH)

Methanol combusts in the presence of oxygen, releasing 726 kJ/mol of energy.

CH₃OH (l) + O₂ (g) → CO₂ (g) + 2 H₂O (l)    ΔH_comb^o = – 726 kJ/mol

2. Propane (C₃H₈)

Propane combusts in the presence of oxygen, releasing 2220 kJ/mol of energy.

C₃H₈ (g) + 5 O₂ (g) → 3 CO₂ (g) + 4 H₂O (l)   ΔH_comb^o = – 2220 kJ/mol

Heating Values of Combustion

The heat of combustion for fuels is expressed as the HHV (Higher Heating Value) or LHV (Lower Heating Value) ^[1-3].

Lower Heating Value assumes that the water formed during a combustion process is in the vapor state after completing the process. Therefore, the energy required to vaporize water is not realized as heat.

Higher Heating Value assumes that all the water in a combustion process is in a liquid state after completion. The enthalpy change for the reaction assumes a common temperature of the substances before and after combustion.

The following table gives the molar heat of combustion or HHV for a few common substances ^[5].

Substance	State	Formula	Molar Heat of Combustion, ΔHcombo (kJ/mol)
Hydrogen	gas	H2	286
Methane	gas	CH4	891
Ethane	gas	C2H6	1561
Propane	gas	C3H8	2220
Butane	gas	C4H10	2878
Pentane	liquid	C5H10	3509
Methanol	liquid	CH3OH	726
Ethanol	liquid	C2H5OH	1367
1-Propanol	liquid	C3H7OH	2021
1-Butanol	liquid	C4H9OH	2676
Acetone	liquid	CH3(CO)CH3	1790
Benzene	liquid	C6H6	3268
Toluene	liquid	C6H5CH3	3910
Carbon (graphite)	solid	C	394

Solved Problems

Problem 1: What is the molar heat of combustion of liquid ethanol (C₂H₅OH)?

Solution

The combustion reaction is

C₂H₅OH (l) + 3 O₂ (g) → 2 CO₂ (g) + 3 H₂O (l)

We use the following formula:

ΔH_comb^o = ΔH_f^o (products) – ΔH_f^o (reactants)

=> ΔH_comb^o = [(2 mol) (ΔH_f^o (CO₂)) + (3 mol) (ΔH_f^o (H₂O))] – [(1 mol) ( ΔH_f^o (C₂H₅OH)) + (3 mol) (ΔH_f^o (O₂))]

Refer to our article on enthalpy of formation for the ΔH_f^o values.

ΔH_f^o (CO₂) (g) = -393.5 kJ/mol, ΔH_f^o (H₂O) (l) = -285.8 kJ/mol, ΔH_f^o (C₂H₅OH) (l) = -277.6 kJ/mol, (ΔH_f^o (O₂) (g) = 0

Therefore,

ΔH_comb^o = [(2 mol) (-393.5 kJ/mol) + (3 mol) (-285.8 kJ/mol)] – [(1 mol) (-277.6 kJ/mol) + (3 mol) (0)] = -1366.8 kJ/mol

Let us convert this into kJ/g.

-1366.8 kJ/mol =-1366.8 kJ/46.1 g = -29.6 kJ/g