The heat of sublimation is the enthalpy change when one gram of a solid directly converts into vapor at a constant temperature. If one mole of the substance transforms, we call the enthalpy change molar heat of sublimation ^[1-4].

Molecular Explanation of Sublimation

A typical household substance is naphthalene balls. When naphthalene balls are in a solid phase, their molecules do not have intermolecular space. The molecules do not have any kinetic energy. It means there is no motion of particles. However, the molecules randomly move when they gain energy, increasing their intermolecular space and changing the solid balls to the gaseous phase ^[2].

How to Calculate Heat of Sublimation

A solid transforms into vapor during sublimation without going through the liquid phase. Energy must be supplied to the substance to sublimate. The energy added goes into doing the following ^[1]:

1. Excite the substance so that it achieves the desired heat capacity at a solid state
2. Break all the intermolecular bonds holding the solid
3. Excited the free molecules so that the solid substance transforms into gas with minimum heat capacity

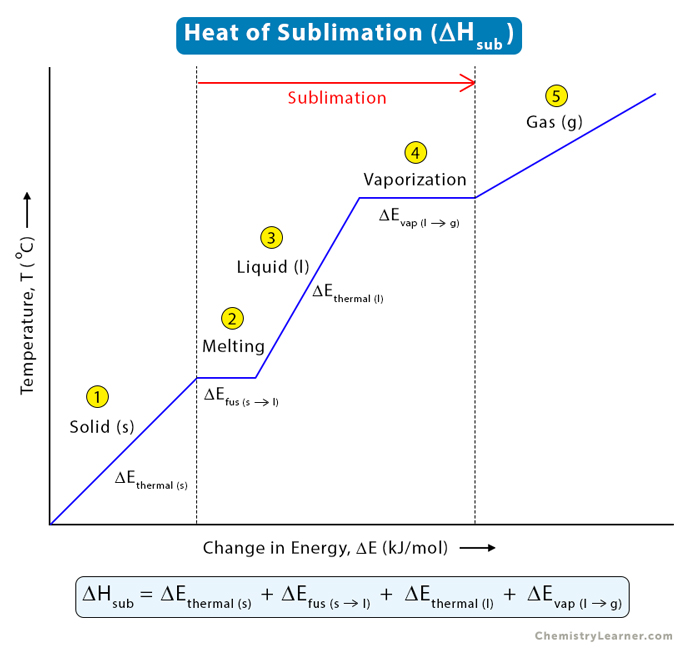
To calculate the heat of sublimation, we construct a temperature vs. energy change graph for the sublimation process. In this graph, we show the fusion and the vaporization stages. Since enthalpy is a state function, we add all the energies associated with the solid, liquid, and gas phases. Let us look at what energies are involved throughout the entire process.

Thermal Energy

When a substance is heated, it absorbs heat. The amount of heat absorbed is given by the change in thermal energy.

ΔE_Thermal = m c_p ΔT

Where

ΔE_Thermal: Change in thermal energy

m: Mass

C_P: Specific heat

ΔT: Change in temperature

Bond Energy

Bond energy is the energy required to separate the molecules so that the substance can undergo a phase change from a lower energy state to a higher energy state. By phase change, we mean melting and vaporization.

ΔE_Bond = (Δm) (ΔH_{phase change})

Where

ΔE_Bond: Bond energy

Δm: Change in mass

ΔH_{phase change}: Enthalpy change due to phase change

Therefore, the various energy changes involved in the sublimation process are:

1. ΔE_{Thermal (s)}: Thermal energy in the solid phase
2. ΔE_{fus (s →l)}: Enthalpy of fusion
3. ΔE_{Thermal (l)}: Thermal energy in the liquid phase
4. ΔE_{vap (l →v)}: Enthalpy of vaporization

The sum of all the energy changes gives the heat of sublimation (ΔH_sub).

ΔH_sub = ΔE_{Thermal (s)} + ΔE_{fus (s →l)} + ΔE_{Thermal (l)} + ΔE_{vap (l →v)}

Unit: J/g or J/mol

Example Problem

Calculate the heat required to convert 1.00 kg of ice with the initial temperature of 273 K into steam at 373 K. Given: heat of fusion = 333.55 kJ/kg, specific heat of water = 4.18 J/g·K, and heat of vaporization = 2257 kJ/kg. Also, calculate the heat of sublimation of 1 mole of ice whose molar mass is 18.02 g.

Solution

Let us break down the sublimation process into various steps.

Step 1: Conversion of 1.00 kg ice into water at 273 K

ΔE_{fus (s → l)} =  333.55 kJ/kg x 1.00 kg = 333.55 kJ

Step 2: Heating of 1.00 kg water from 273 K to 373 K

ΔE_{thermal (l)} = m c_P ΔT = 1000 g x 4.18 J/g·K x (373 K – 273 K) = 418 kJ

Step 3: Conversion of 1.00 kg water into steam at 373 K

ΔE_{vap (l → g)} = 2257 kJ/kg x 1.00 kg = 2257 kJ

The heat necessary is

ΔH_sub = ΔE_{fus (s → l)} + ΔE_{thermal (l)} + ΔE_{vap (l → g)} = 333.55 kJ + 418 kJ + 2257 kJ = 3008 kJ

The molar heat of sublimation of ice is

ΔH_sub = 3008 kJ/kg x 18.02 x 10^-3 kg/mol = 54.2 kJ/mol