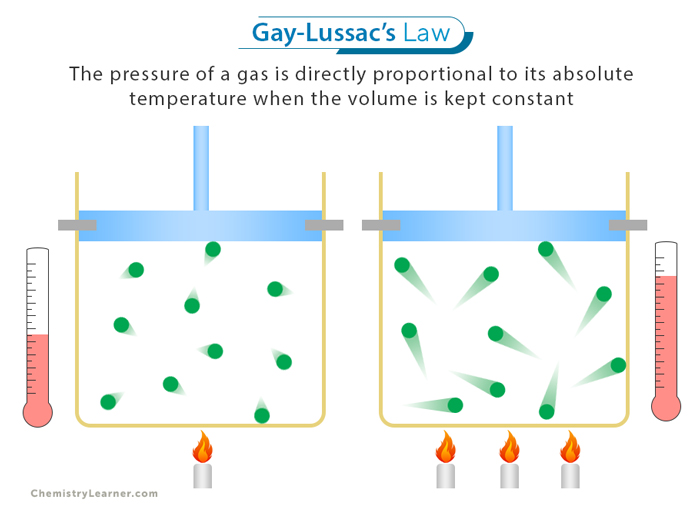
Gay-Lussac’s Law elucidates a critical relationship between pressure and temperature in a confined gas system. The law asserts that, at constant volume and mass, the pressure of a gas is directly proportional to its absolute temperature. This simple yet profound relationship forms a cornerstone in the study of gas properties, offering valuable insights into the dynamic nature of gases. This relationship has profound implications in thermodynamics, where a comprehensive understanding of gas properties is essential. ^[1-4]

This law is named after the French chemist Joseph Gay-Lussac, who formulated it in 1808.

Formula

Mathematically, the law is represented as ^[1-4]

P/T = k

Where

P is the pressure of the gas

T is its absolute temperature

k is a constant.

In other words, when the pressure of a gas increases, its temperature also increases proportionally, provided the volume and the amount of gas remain constant.

This formula embodies the fundamental relationship between pressure and temperature in a confined gas system, holding under constant volume and mass. The direct proportionality between pressure and temperature signifies that as the temperature of a gas increases, so does its pressure, and vice versa. As the gas temperature rises, the gas molecules gain kinetic energy, leading to more frequent and forceful collisions with the container walls, thereby increasing the pressure.

The constant ‘k’ maintains the proportional relationship between pressure and temperature. This constant signifies that the ratio of pressure to temperature remains constant for a given amount of gas under constant volume conditions. The value of ‘k’ can vary depending on the specific gas being studied, and it serves as a unique identifier for that particular gas system.

This straightforward relationship is crucial for understanding the dynamic behavior of gases and is particularly applicable in scenarios where pressure and temperature changes need to be predicted and controlled, such as in industrial processes and weather-related phenomena. Thus, the law serves as a guiding principle in comprehending the intricacies of gas behavior under varying thermal conditions.

Alternative Form of the Equation

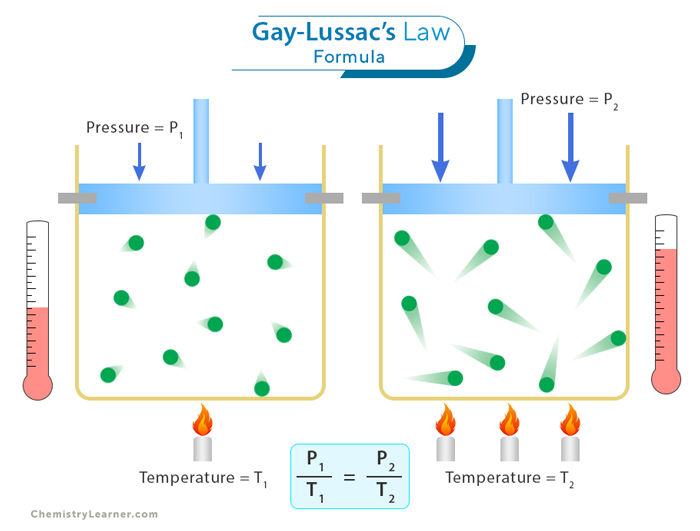
Another way of expressing Gay-Lussac’s Law is as follows:

​P₁/T₁​ ​​= P₂/T₂​

Where:

P_1​ is the pressure of the gas at state 1

T₁​ is the absolute temperature of the gas at state 1

P₂​ is the pressure of the gas at state 2

T₂​ is the absolute temperature of the gas at state 2

This equation illustrates the proportional relationship between the pressure and temperature of a gas during two states. Here, the volume and the amount of gas are kept constant. It signifies that the ratio of pressure to temperature remains constant for a given amount of gas in these conditions.

Graph

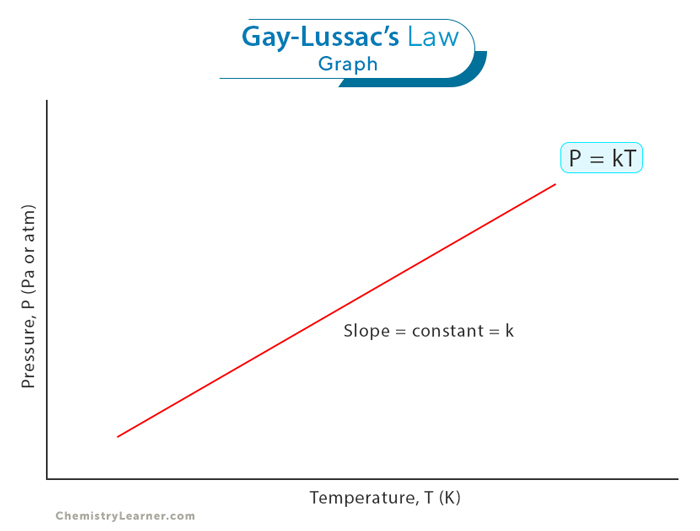
The graphical representation of Gay-Lussac’s Law serves as a powerful visual tool to illustrate the linear relationship between pressure and temperature in a confined gas system. The result is a straight line when this relationship is plotted on a graph, with pressure on the y-axis and temperature on the x-axis. This linear correlation reflects the proportional nature of Gay-Lussac’s Law, emphasizing the predictability of how a gas will respond to changes in temperature under constant volume conditions. ^[1-4]

Example

When subjected to heat, a pressurized aerosol can, like those used for deodorants or spray paint, undergoes an elevation in pressure as per Gay-Lussac’s law. This pressure surge applied by the container gases can potentially lead to an explosion. Consequently, numerous pressurized containers carry warning labels instructing users to keep them away from open flames and store them in cool environments to mitigate the risk of such incidents.

Solved Problems

Problem 1: A sample of gas is initially at a pressure of 2.0 atm and a temperature of 300 K. If the temperature is increased to 400 K while keeping the volume constant, what will be the new pressure?

Solution:

Using Gay-Lussac’s Law, we can set up the equation:

​P₁/T₁​ ​​= P₂/T₂​

Given: ​P₁ = 2.0 atm, ​T₁ = 300 K, and ​T₂ = 400 K.

2.0 atm/300 K ​​= P₂/400 K

Solving for P₂

 P₂ = 2.0 atm x (400 K/300 K) 

=>  P₂ = 2.67 atm

Problem 2: If a gas at 3.5 atm pressure and 400 K temperature undergoes a temperature decrease to 300 K while keeping the volume constant, what will be the new pressure?

Solution:

Applying Gay-Lussac’s Law, the equation is:

​P₁/T₁​ ​​= P₂/T₂

Given that P₁ = 3.5 atm, T₁ = 400 K, and T₂ = 300 K, we want to find P₂

​3.5 atm/400 K​ ​​= P₂/300 K

Solving for P₂:

P₂ = 3.5 atm x 300 K/400 K

=> P₂ = 2.625 atm